Pi Formulas
There are many formulas of
series, products, geometric constructions, limits, special values, and pi
iterations.
and spheres. For a circle of radius
and area are given by
(1) | |||
(2) |
and volume enclosed are
(3) | |||
(4) |
tangents of unit fractions is Machin's
formula
(5) |
as well as thousands of other similar formulas having more terms.
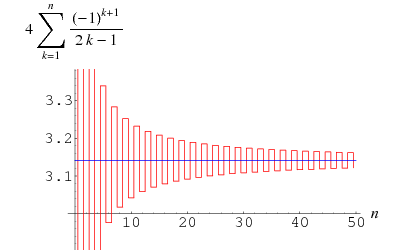
Gregory and Leibniz found
(6) | |||
(7) |
after the
series is larger than
that 300 terms are not sufficient to calculate
decimal places! However, it can be transformed to
(8) |
zeta function (Vardi 1991, pp. 157-158; Flajolet and Vardi 1996), so that
the error after
An infinite sum series to Abraham Sharp (ca. 1717) is given by
(9) |
(10) | |||
(11) | |||
(12) | |||
(13) | |||
(14) | |||
(15) | |||
(16) | |||
(17) |
In 1666, Newton used a geometric construction to derive the formula
(18) | |||
(19) |
al. 1989; Borwein and Bailey 2003, pp. 105-106). The coefficients can be
found from the integral
(20) | |||
(21) |
0, obtaining
(22) |
transformation gives
(23) | |||
(24) | |||
(25) |
This corresponds to plugging
the power series for the hypergeometric
function
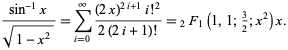 | (26) |
(27) |
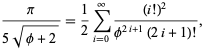 | (28) |
ratio. Gosper also obtained
(29) |
and Wagon (1995; Borwein and Bailey 2003, pp. 141-142).
More amazingly still, a closed form expression giving a digit-extraction algorithm which produces digits of
was discovered by Bailey et al. (Bailey et al. 1997, Adamchik and Wagon
1997),
(30) |
and is equivalent to
(31) |
few independent formulas of which are
(32) | |||
(33) | |||
(34) | |||
![sum_(k=0)^(infty)(-1)^k[3/(14k+1)-3/(14k+3)+3/(14k+5)+4/(14k+7)+4/(14k+9)-4/(14k+11)+4/(14k+13)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline101.gif) | (35) | ||
![sum_(k=0)^(infty)(-1)^k[2/(18k+1)+3/(18k+3)+2/(18k+5)-2/(18k+7)-2/(18k+11)+2/(18k+13)+3/(18k+15)+2/(18k+17)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline104.gif) | (36) | ||
![sum_(k=0)^(infty)(-1)^k[3/(22k+1)-3/(22k+3)+3/(22k+5)-3/(22k+7)+3/(22k+9)+8/(22k+11)+3/(22k+13)-3/(22k+15)+3/(22k+17)-3/(22k+19)+1/(22k+21)].](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline107.gif) | (37) |
independent formulas of which are
(38) | |||
(39) | |||
![1/(16)sum_(k=0)^(infty)1/(256^k)[(64)/(16k+1)-(32)/(16k+4)-(16)/(16k+5)-(16)/(16k+6)+4/(16k+9)-2/(16k+12)-1/(16k+13)-1/(16k+14)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline118.gif) | (40) | ||
![1/(32)sum_(k=0)^(infty)1/(256^k)[(128)/(16k+2)+(64)/(16k+3)+(64)/(16k+4)-(16)/(16k+7)+8/(16k+10)+4/(16k+11)+4/(16k+12)-1/(16k+15)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline121.gif) | (41) | ||
![1/(32)sum_(k=0)^(infty)1/(4096^k)[(256)/(24k+2)+(192)/(24k+3)-(256)/(24k+4)-(96)/(24k+6)-(96)/(24k+8)+(16)/(24k+10)-4/(24k+12)-3/(24k+15)-6/(24k+16)-2/(24k+18)-1/(24k+20)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline124.gif) | (42) | ||
![1/(64)sum_(k=0)^(infty)1/(4096^k)[(256)/(24k+1)+(256)/(24k+2)-(384)/(24k+3)-(256)/(24k+4)-(64)/(24k+5)+(96)/(24k+8)+(64)/(24k+9)+(16)/(24k+10)+8/(24k+12)-4/(24k+13)+6/(24k+15)+6/(24k+16)+1/(24k+17)+1/(24k+18)-1/(24k+20)-1/(24k+21)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline127.gif) | (43) | ||
![1/(96)sum_(k=0)^(infty)1/(4096^k)[(256)/(24k+2)+(64)/(24k+3)+(128)/(24k+5)+(352)/(24k+6)+(64)/(24k+7)+(288)/(24k+8)+(128)/(24k+9)+(80)/(24k+10)+(20)/(24k+12)-(16)/(24k+14)-1/(24k+15)+6/(24k+16)-2/(24k+17)-1/(24k+19)+1/(24k+20)-2/(24k+21)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline130.gif) | (44) | ||
![1/(96)sum_(k=0)^(infty)1/(4096^k)[(256)/(24k+1)+(320)/(24k+3)+(256)/(24k+4)-(192)/(24k+5)-(224)/(24k+6)-(64)/(24k+7)-(192)/(24k+8)-(64)/(24k+9)-(64)/(24k+10)-(28)/(24k+12)-4/(24k+13)-5/(24k+15)+3/(24k+17)+1/(24k+18)+1/(24k+19)+1/(24k+21)-1/(24k+22)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline133.gif) | (45) | ||
![1/(96)sum_(k=0)^(infty)1/(4096^k)[(512)/(24k+1)-(256)/(24k+2)+(64)/(24k+3)-(512)/(24k+4)-(32)/(24k+6)+(64)/(24k+7)+(96)/(24k+8)+(64)/(24k+9)+(48)/(24k+10)-(12)/(24k+12)-8/(24k+13)-(16)/(24k+14)-1/(24k+15)-6/(24k+16)-2/(24k+18)-1/(24k+19)-1/(24k+20)-1/(24k+21)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline136.gif) | (46) | ||
![1/(4096)sum_(k=0)^(infty)1/(65536^k)[(16384)/(32k+1)-(8192)/(32k+4)-(4096)/(32k+5)-(4096)/(32k+6)+(1024)/(32k+9)-(512)/(32k+12)-(256)/(32k+13)-(256)/(32k+14)+(64)/(32k+17)-(32)/(32k+20)-(16)/(32k+21)-(16)/(32k+22)+4/(32k+25)-2/(32k+28)-1/(32k+29)-1/(32k+30)]](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline139.gif) | (47) | ||
![1/(4096)sum_(k=0)^(infty)1/(65536^k)[(32768)/(32k+2)+(16384)/(32k+3)+(16384)/(32k+4)-(4096)/(32k+7)+(2048)/(32k+10)+(1024)/(32k+11)+(1024)/(32k+12)-(256)/(32k+15)+(128)/(32k+18)+(64)/(32k+19)+(64)/(32k+20)-(16)/(32k+23)+8/(32k+26)+4/(32k+27)+4/(32k+28)-1/(32k+31)].](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline142.gif) | (48) |
formula
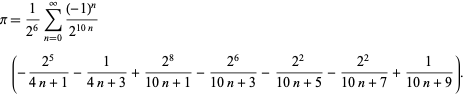 | (49) |
(50) |
Girgensohn 2004, p. 3; Boros and Moll 2004, p. 125; Lucas 2005; Borwein et al.
2007, p. 14). This integral was known by K. Mahler in the mid-1960s
and appears in an exam at the University of Sydney in November 1960 (Borwein, Bailey,
and Girgensohn, p. 3). Beukers (2000) and Boros and Moll (2004, p. 126)
state that it is not clear if these exists a natural choice of rational polynomial
whose integral between 0 and 1 produces
333/106 is the next convergent. However, an integral exists for the fourth
convergent, namely
(51) |
a few other such integrals.
Backhouse (1995) used the identity
(52) | |||
(53) | |||
(54) |
to generate a number of formulas for
if
A similar formula was subsequently discovered by Ferguson, leading to a
two-dimensional lattice of such formulas which can be generated by these
two formulas given by
(55) |
formula as the special case
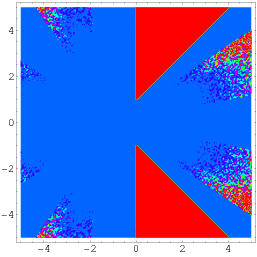
An even more general identity due to Wagon is given by
![pi+4tan^(-1)z+2ln((1-2z-z^2)/(z^2+1))=sum_(k=0)^infty1/(16^k)[(4(z+1)^(8k+1))/(8k+1)-(2(z+1)^(8k+4))/(8k+4)-((z+1)^(8k+5))/(8k+5)-((z+1)^(8k+6))/(8k+6)]](http://mathworld.wolfram.com/images/equations/PiFormulas/NumberedEquation15.gif) | (56) |
axis, as illustrated above.
A perhaps even stranger general class of identities is given by
![pi=4sum_(j=1)^n((-1)^(j+1))/(2j-1)+((-1)^n(2n-1)!)/4sum_(k=0)^infty1/(16^k)[8/((8k+1)_(2n))-4/((8k+3)_(2n))-4/((8k+4)_(2n))-2/((8k+5)_(2n))+1/((8k+7)_(2n))+1/((8k+8)_(2n))]](http://mathworld.wolfram.com/images/equations/PiFormulas/NumberedEquation16.gif) | (57) |
symbol (B. Cloitre, pers. comm., Jan. 23, 2005). Even more amazingly,
there is a closely analogous formula for the natural
logarithm of 2.
Following the discovery of the base-16 digit BBP formula and related formulas, similar formulas in other bases were investigated. Borwein,
Bailey, and Girgensohn (2004) have recently shown that
BBP arctangent formula that is not binary, although this does not rule out a completely
different scheme for digit-extraction algorithms
in other bases.
S. Plouffe has devised an algorithm to compute the
of
A slew of additional identities due to Ramanujan, Catalan, and Newton
are given by Castellanos (1988ab, pp. 86-88), including several
involving sums of Fibonacci
numbers. Ramanujan found
![sum_(k=0)^infty((-1)^k(4k+1)[(2k-1)!!]^3)/([(2k)!!]^3)=sum_(k=0)^infty((-1)^k(4k+1)[Gamma(k+1/2)]^3)/(pi^(3/2)[Gamma(k+1)]^3)=2/pi](http://mathworld.wolfram.com/images/equations/PiFormulas/NumberedEquation17.gif) | (58) |
Plouffe (2006) found the beautiful formula
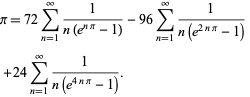 | (59) |
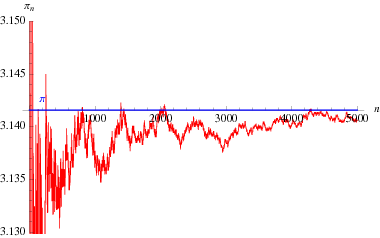
An interesting infinite product formula due to Euler which relates
![2/(product_(n=1)^(infty)[1+(sin(1/2pip_n))/(p_n)])](http://mathworld.wolfram.com/images/equations/PiFormulas/Inline174.gif) | (60) | ||
(61) |
A method similar to Archimedes' can be used to estimate
an
of subsequent
from the center of one of the polygon's segments,
(62) |
(63) |
Vieta (1593) was the first to give an exact expression for
(64) |
radicals,
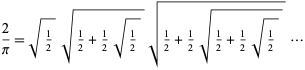 | (65) |
A related formula is given by
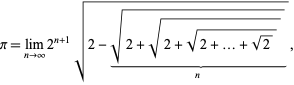 | (66) |
(67) |
![pi_n=sqrt((1/2pi_(n-1))^2+[1-sqrt(1-(1/2pi_(n-1))^2)]^2)](http://mathworld.wolfram.com/images/equations/PiFormulas/NumberedEquation25.gif) | (68) |
comm., April 27, 2000). The formula
![pi=2lim_(m->infty)sum_(n=1)^msqrt([sqrt(1-((n-1)/m)^2)-sqrt(1-(n/m)^2)]^2+1/(m^2))](http://mathworld.wolfram.com/images/equations/PiFormulas/NumberedEquation26.gif) | (69) |
A pretty formula for
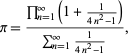 | (70) |
sum with sum 1/2 since
(71) |
A particular case of the Wallis formula gives
(72) |
![lim_(n->infty)(2^(4n))/(n(2n; n)^2)=pilim_(n->infty)(n[Gamma(n)]^2)/([Gamma(1/2+n)]^2)=pi,](http://mathworld.wolfram.com/images/equations/PiFormulas/NumberedEquation30.gif) | (73) |
coefficient and
function (Knopp 1990). Euler obtained
(74) |
follow from
integers
An infinite sum due to Ramanujan is
(75) |
2007, p. 44). Further sums are given in Ramanujan (1913-14),
(76) |
(77) | |||
(78) |
is derived from a modular identity of order 58, although a first derivation was not
presented prior to Borwein and Borwein (1987). The above series both give
(79) |
respectively, about 6 and 8 decimal places per term. Such series exist
because of the rationality of various modular invariants.
The general form of the series is
(80) |
quadratic form discriminant,
(81) | |||
(82) |
series. A class number
integers of the constants
terms, the one gives the most numeric digits in the shortest period of time corresponds
to the largest class number 1 discriminant of
(1987). The 163 appearing here is the same one appearing in the fact that
(the Ramanujan constant) is very nearly an
integer. Similarly, the factor
the j-function identity for
The series is given by
(83) | |||
(84) |
was given by the Chudnovsky brothers (1987) and is used by the Wolfram
Language to calculate
(85) |
(86) | |||
(87) | |||
(88) |
(89) |
(90) | |||
(91) | |||
(92) |
3 corresponds to
The fastest converging class number 4 series corresponds
to
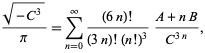 | (93) |
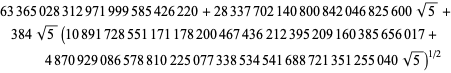 | (94) | ||
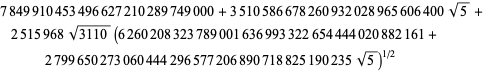 | (95) | ||
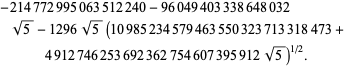 | (96) |
class number.
A complete listing of Ramanujan's series for
second and third notebooks is given by Berndt (1994, pp. 352-354),
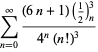 | (97) | ||
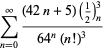 | (98) | ||
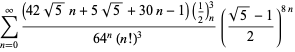 | (99) | ||
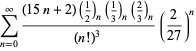 | (100) | ||
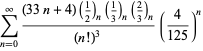 | (101) | ||
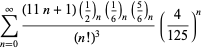 | (102) | ||
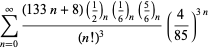 | (103) | ||
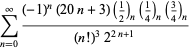 | (104) | ||
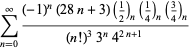 | (105) | ||
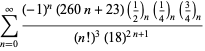 | (106) | ||
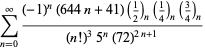 | (107) | ||
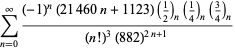 | (108) | ||
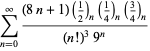 | (109) | ||
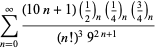 | (110) | ||
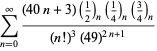 | (111) | ||
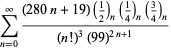 | (112) | ||
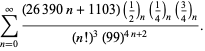 | (113) |
pp. 177-187). Borwein and Borwein (1987b, 1988, 1993) proved other
equations of this type, and
Chudnovsky and Chudnovsky (1987) found similar equations for other
transcendental
constants (Bailey et al. 2007, pp. 44-45).
A complete list of independent known equations of this type is given by
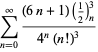 | (114) | ||
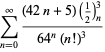 | (115) | ||
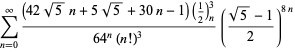 | (116) | ||
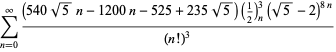 | (117) | ||
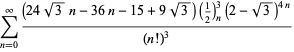 | (118) |
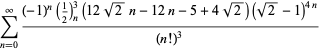 | (119) | ||
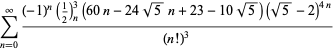 | (120) | ||
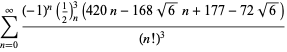 | (121) | ||
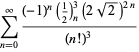 | (122) |
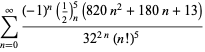 | (123) | ||
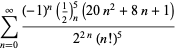 | (124) |
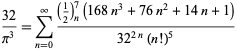 | (125) |
Bellard gives the exotic formula
![pi=1/(740025)[sum_(n=1)^infty(3P(n))/((7n; 2n)2^(n-1))-20379280],](http://mathworld.wolfram.com/images/equations/PiFormulas/NumberedEquation40.gif) | (126) |
(127) |
(128) |
hypergeometric function, and transforms it to
(129) |
(130) |
(131) |
(132) |
SEE ALSO: BBP Formula, Digit-Extraction Algorithm, Pi, Pi Approximations,
Pi Continued Fraction, Pi
Digits, Pi Iterations, Pi
Squared, Spigot Algorithm
REFERENCES:
Adamchik, V. and Wagon, S. "A Simple Formula for 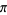 ." Amer.
." Amer.
Math. Monthly 104, 852-855, 1997.
Math. Monthly 104, 852-855, 1997.
Adamchik, V. and Wagon, S. "Pi: A 2000-Year Search Changes Direction."
http://www-2.cs.cmu.edu/~adamchik/articles/pi.htm.
http://www-2.cs.cmu.edu/~adamchik/articles/pi.htm.
Backhouse, N. "Note 79.36. Pancake Functions and Approximations to 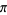 ." Math.
." Math.
Gaz. 79, 371-374, 1995.
Gaz. 79, 371-374, 1995.
Bailey, D. H. "Numerical Results on the Transcendence of Constants Involving 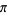 ,
, 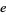 , and Euler's Constant."
, and Euler's Constant."
Math. Comput. 50, 275-281, 1988a.
Math. Comput. 50, 275-281, 1988a.
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental
Mathematics in Action. Wellesley, MA: A K Peters, 2007.
Mathematics in Action. Wellesley, MA: A K Peters, 2007.
Bailey, D. H.; Borwein, P.; and Plouffe, S. "On the Rapid Computation of Various Polylogarithmic Constants." Math. Comput. 66, 903-913,
1997.
1997.
Beck, G. and Trott, M. "Calculating Pi: From Antiquity to Moderns Times."
http://documents.wolfram.com/mathematica/Demos/Notebooks/CalculatingPi.html.
http://documents.wolfram.com/mathematica/Demos/Notebooks/CalculatingPi.html.
Beckmann, P. A
History of Pi, 3rd ed. New York: Dorset Press, 1989.
History of Pi, 3rd ed. New York: Dorset Press, 1989.
Beeler, M. et al. Item 140 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239,
p. 69, Feb. 1972. http://www.inwap.com/pdp10/hbaker/hakmem/pi.html#item140.
p. 69, Feb. 1972. http://www.inwap.com/pdp10/hbaker/hakmem/pi.html#item140.
Berndt, B. C. Ramanujan's
Notebooks, Part IV. New York: Springer-Verlag, 1994.
Notebooks, Part IV. New York: Springer-Verlag, 1994.
Beukers, F. "A Rational Approximation to 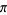 ." Nieuw
." Nieuw
Arch. Wisk. 5, 372-379, 2000.
Arch. Wisk. 5, 372-379, 2000.
Blatner, D. The
Joy of Pi. New York: Walker, 1997.
Joy of Pi. New York: Walker, 1997.
Boros, G. and Moll, V. Irresistible Integrals: Symbolics, Analysis and Experiments in the Evaluation of Integrals.
Cambridge, England: Cambridge University Press, 2004.
Cambridge, England: Cambridge University Press, 2004.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A
K Peters, 2003.
K Peters, 2003.
Borwein, J.; Bailey, D.; and Girgensohn, R. Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters,
2004.
2004.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity.
New York: Wiley, 1987a.
New York: Wiley, 1987a.
Borwein, J. M. and Borwein, P. B. "Ramanujan's Rational and Algebraic Series for 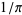 ." Indian J. Math. 51,
." Indian J. Math. 51,
147-160, 1987b.
147-160, 1987b.
Borwein, J. M. and Borwein, P. B. "More Ramanujan-Type Series for 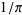 ." In Ramanujan
." In Ramanujan
Revisited: Proceedings of the Centenary Conference, University of Illinois at Urbana-Champaign,
June 1-5, 1987 (Ed. G. E. Andrews, B. C. Berndt, and
R. A. Rankin). New York: Academic Press, pp. 359-374, 1988.
Revisited: Proceedings of the Centenary Conference, University of Illinois at Urbana-Champaign,
June 1-5, 1987 (Ed. G. E. Andrews, B. C. Berndt, and
R. A. Rankin). New York: Academic Press, pp. 359-374, 1988.
Borwein, J. M. and Borwein, P. B. "Class Number Three Ramanujan Type Series for 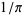 ." J. Comput. Appl. Math. 46,
." J. Comput. Appl. Math. 46,
281-290, 1993.
281-290, 1993.
Borwein, J. M.; Borwein, P. B.; and Bailey, D. H. "Ramanujan, Modular
Equations, and Approximations to Pi, or How to Compute One Billion
Digits
of Pi." Amer. Math. Monthly 96, 201-219, 1989.
Equations, and Approximations to Pi, or How to Compute One Billion
Digits
of Pi." Amer. Math. Monthly 96, 201-219, 1989.
Borwein, J. M.; Borwein, D.; and Galway, W. F. "Finding and Excluding 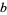 -ary Machin-Type Individual Digit Formulae."
-ary Machin-Type Individual Digit Formulae."
Canad. J. Math. 56, 897-925, 2004.
Canad. J. Math. 56, 897-925, 2004.
Castellanos, D. "The Ubiquitous Pi. Part I." Math. Mag. 61,
67-98, 1988a.
67-98, 1988a.
Castellanos, D. "The Ubiquitous Pi. Part II." Math. Mag. 61,
148-163, 1988b.
148-163, 1988b.
Chudnovsky, D. V. and Chudnovsky, G. V. "Approximations and Complex Multiplication According to Ramanujan." In Ramanujan
Revisited: Proceedings of the Centenary Conference, University of Illinois at Urbana-Champaign,
June 1-5, 1987 (Ed. G. E. Andrews, B. C. Berndt, and
R. A. Rankin). Boston, MA: Academic Press, pp. 375-472, 1987.
Revisited: Proceedings of the Centenary Conference, University of Illinois at Urbana-Champaign,
June 1-5, 1987 (Ed. G. E. Andrews, B. C. Berndt, and
R. A. Rankin). Boston, MA: Academic Press, pp. 375-472, 1987.
Dalzell, D. P. "On 22/7." J. London Math. Soc. 19, 133-134,
1944.
1944.
Dalzell, D. P. "On 22/7 and 355/113." Eureka 34, 10-13,
1971.
1971.
Ferguson, H. R. P.; Bailey, D. H.; and Arno, S. "Analysis of PSLQ, An Integer Relation Finding Algorithm." Math. Comput. 68,
351-369, 1999.
351-369, 1999.
Finch, S. R. Mathematical
Constants. Cambridge, England: Cambridge University Press, 2003.
Constants. Cambridge, England: Cambridge University Press, 2003.
Flajolet, P. and Vardi, I. "Zeta Function Expansions of Classical Constants."
Unpublished manuscript. 1996. http://algo.inria.fr/flajolet/Publications/landau.ps.
Unpublished manuscript. 1996. http://algo.inria.fr/flajolet/Publications/landau.ps.
Gasper, G. "Re: confluent pi." math-fun@cs.arizona.edu posting, Aug. 18, 1996.
Gosper, R. W. math-fun@cs.arizona.edu posting, Sept. 1996.
Gosper, R. W. "a product." math-fun@cs.arizona.edu posting,
Sept. 27, 1996.
Sept. 27, 1996.
Gourdon, X. and Sebah, P. "Collection of Series for 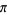 ." http://numbers.computation.free.fr/Constants/Pi/piSeries.html.
." http://numbers.computation.free.fr/Constants/Pi/piSeries.html.
Guillera, J. "Some Binomial Series Obtained by the WZ-Method." Adv.
Appl. Math. 29, 599-603, 2002.
Appl. Math. 29, 599-603, 2002.
Guillera, J. "About a New Kind of Ramanujan-Type Series." Exp. Math. 12,
507-510, 2003.
507-510, 2003.
Guillera, J. "Generators of Some Ramanujan Formulas." Ramanujan J. 11,
41-48, 2006.
41-48, 2006.
Hardy, G. H. "A Chapter from Ramanujan's Note-Book." Proc. Cambridge
Philos. Soc. 21, 492-503, 1923.
Philos. Soc. 21, 492-503, 1923.
Hardy, G. H. "Some Formulae of Ramanujan." Proc. London Math. Soc.
(Records of Proceedings at Meetings) 22, xii-xiii, 1924.
(Records of Proceedings at Meetings) 22, xii-xiii, 1924.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York:
Chelsea, 1999.
Chelsea, 1999.
Le Lionnais, F. Les
nombres remarquables. Paris: Hermann, 1983.
nombres remarquables. Paris: Hermann, 1983.
Lucas, S. K. "Integral Proofs that 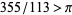 ."
."
Austral. Math. Soc. Gaz. 32, 263-266, 2005.
Austral. Math. Soc. Gaz. 32, 263-266, 2005.
MathPages. "Rounding Up to Pi." http://www.mathpages.com/home/kmath001.htm.
Plouffe, S. "Identities Inspired from Ramanujan Notebooks (Part 2)." Apr. 2006.
http://www.lacim.uqam.ca/~plouffe/inspired2.pdf.
http://www.lacim.uqam.ca/~plouffe/inspired2.pdf.
Rabinowitz, S. and Wagon, S. "A Spigot Algorithm for the Digits of 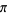 ." Amer.
." Amer.
Math. Monthly 102, 195-203, 1995.
Math. Monthly 102, 195-203, 1995.
Ramanujan, S. "Modular Equations and Approximations to 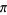 ." Quart.
." Quart.
J. Pure. Appl. Math. 45, 350-372, 1913-1914.
J. Pure. Appl. Math. 45, 350-372, 1913-1914.
Smith, D. History
of Mathematics, Vol. 2. New York: Dover, 1953.
of Mathematics, Vol. 2. New York: Dover, 1953.
Sondow, J. "Problem 88." Math Horizons, pp. 32 and 34, Sept. 1997.
Sondow, J. "A Faster Product for 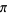 and a New Integral
and a New Integral
for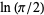 ." Amer. Math. Monthly 112,
." Amer. Math. Monthly 112,
729-734, 2005.
for
729-734, 2005.
Vardi, I. Computational
Recreations in Mathematica. Reading, MA: Addison-Wesley, p. 159, 1991.
Recreations in Mathematica. Reading, MA: Addison-Wesley, p. 159, 1991.
Vieta, F. Uriorum de rebus mathematicis responsorum. Liber VII. 1593. Reprinted
in New York: Georg Olms, pp. 398-400 and 436-446, 1970.
in New York: Georg Olms, pp. 398-400 and 436-446, 1970.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England:
Penguin Books, 1986.
Penguin Books, 1986.
Wolfram Research, Inc. "Some Notes On Internal Implementation: Mathematical
Constants." http://reference.wolfram.com/language/tutorial/SomeNotesOnInternalImplementation.html.
Referenced on Wolfram|Alpha: Pi FormulasConstants." http://reference.wolfram.com/language/tutorial/SomeNotesOnInternalImplementation.html.
CITE THIS AS:
Weisstein, Eric W. "Pi Formulas." From
MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/PiFormulas.html
MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/PiFormulas.html
Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου